Pernahkah Anda mendengar atau tahu tentang statistik bayesian?
Melansir laman Research Connections, statistik bayesian adalah pendekatan umum untuk memperkirakan parameter populasi (karakteristik) yang menggunakan informasi tentang distribusi sebelumnya dari parameter yang diinginkan serta bukti baru (fungsi kemungkinan).
Dalam statistik bayesian, distribusi probablitas posterior adalah distribusi probabilitas setelah semua informasi diperhitungkan.
Apa Itu Statistik Bayesian?

Statistik bayesian telah lama dianggap sebagai cabang ilmu statistik, tetapi peran dan dampaknya terhadap pengembangan inferensi atau simpulan statistik jauh lebih besar.
Saat ini, statistik bayesian dianggap sebagai studi tentang peristiwa yang tidak pasti melalui gagasan probabilitas. Tujuannya adalah pengembangan metodologi yang koheren untuk penalaran matematis induktif.
Nama metode ini yaitu dari Thomas Bayes, seorang ahli matematika abad ke-18. Dalam statistik klasik (atau frekuensialis), probabilitas dianggap sebagai frekuensi relatif dari suatu peristiwa dalam jumlah percobaan yang sangat besar.
Sebaliknya, dalam pendekatan Bayesian, probabilitas dianggap sebagai ukuran keyakinan atau ketidakpastian tentang suatu peristiwa.
Baca juga: Analisis Pasar: Definisi, Tujuan, Cara Melakukannya
Konsep Utama Statistik Bayesian
Terdapat beberapa konsep utama dalam statistik bayesian, di antaranya:
1. Prior Probability (Probabilitas Awal)
Merupakayan keyakinan awal atau distribusi probabilitas sebelum diperolehnya data tambahan. Prior ini merefleksikan pengetahuan atau keyakinan awal kita tentang parameter yang sedang dipelajari.
2. Likelihood (Peluang)
Ini merupakan distribusi probabilitas dari data yang diberikan parameter. Memberikan informasi tentang sejauh mana parameter dapat menjelaskan data yang diamati.
3. Posterior Probability (Probabilitas Posterior)
Merupakan distribusi probabilitas yang diperbarui setelah menggabungkan informasi dari prior dan likelihood. Posterior probability menggambarkan keyakinan kita tentang parameter setelah memperhitungkan data yang diamati.
4. Teorema Bayes
Yaitu hubungan antara prior, likelihood, dan posterior dinyatakan dalam Teorema Bayes. Secara matematis, teorema Bayes dapat ditulis sebagai berikut:
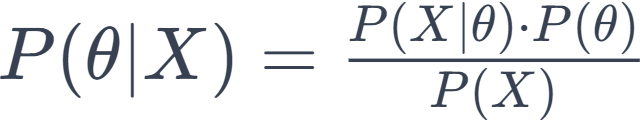
di mana:
- P(θ∣X) adalah posterior probability dari parameter θ setelah melihat data X.
- P(X∣θ) adalah likelihood dari data X dengan parameter θ.
- P(θ) adalah prior probability dari parameter θ.
- P(X) adalah probability dari data X.
5. Inferensi Bayesian
Dengan menggunakan Teorema Bayes, kita dapat melakukan inferensi tentang parameter yang tidak diketahui berdasarkan data yang diperoleh dan pengetahuan awal yang kita miliki.
Baca juga: Observasi Langsung: Penjelasan, Tujuan, hingga Contoh
Kegunaan Statistik Bayesian dalam Riset Pasar

Penggunaan statistik bayesian dalam proses penelitian atau riset pasar dapat memberikan beberapa manfaat signifikan, contohnya seperti:
1. Keputusan yang Dapat Diterima
Estimasi bayesian sering kali disajikan dalam bentuk distribusi probabilitas yang dapat membantu pengambil keputusan memahami tingkat ketidakpastian dan membuat keputusan lebih informasional.
2. Fleksibilitas Model
Metode bayesian memberikan fleksibilitas dalam memodelkan distribusi posterior parameter. Ini memungkinkan peneliti untuk membangun model yang lebih kompleks dan lebih sesuai dengan sifat unik dari data riset pasar.
3. Peramalan Lebih Akurat
Dengan kemampuan untuk memperbarui model seiring waktu, bayesian dapat memberikan peramalan yang lebih akurat dan responsif terhadap perubahan dalam perilaku konsumen atau pasar.
4. Integrasi Informasi Awal
Statistik bayesian memungkinkan peneliti mengintegrasikan pengetahuan awal atau keyakinan sebelumnya ke dalam analisis.
Hal ini dapat mencakup hasil riset sebelumnya, pandangan ahli, atau informasi pasar yang sudah ada. Integrasi informasi awal ini membantu memberikan hasil yang lebih akurat dan konsisten.
5. Menghemat Sumber Daya
Menggunakan bayesian, peneliti dapat lebih efisien dalam penggunaan sumber daya karena mereka dapat memanfaatkan informasi sebelumnya dan mengoptimalkan desain studi atau riset pasar.
***
Statistik Bayesian bukan sekadar alat analisis data, tetapi juga suatu pendekatan yang dapat mengoptimalkan keputusan bisnis.
Dalam konteks riset pasar, penerapan statistik bayesian membuka peluang baru untuk memahami preferensi konsumen, merancang strategi pemasaran yang lebih efektif, dan mengambil keputusan yang lebih tepat berdasarkan informasi yang lebih akurat.
Dengan memanfaatkan kekuatan statistik bayesian, perusahaan dapat meningkatkan daya saing mereka di pasar yang kompetitif dan mengoptimalkan hasil riset pasar untuk mencapai kesuksesan jangka panjang.

Baca juga: Ukuran Penyebaran: Definisi, Jenis, Contoh dalam Penelitian

 IDN
IDN
 ENG
ENG 


